核方法思想

参考阅读：核函数

简单来说，核函数就是我们需要将数据进行高维非线性映射时，减少计算量的一种运算技巧，核函数的选取决定了映射空间的质量，所以有了多核学习，其实就是多种核函数的组合（构成一个加权求和核），通过学习得出一个合适的组合系数

案例1，通过非线性映射函数将原始空间中的线性不可分数据映射到目标空间，从而变得线性可分¹：

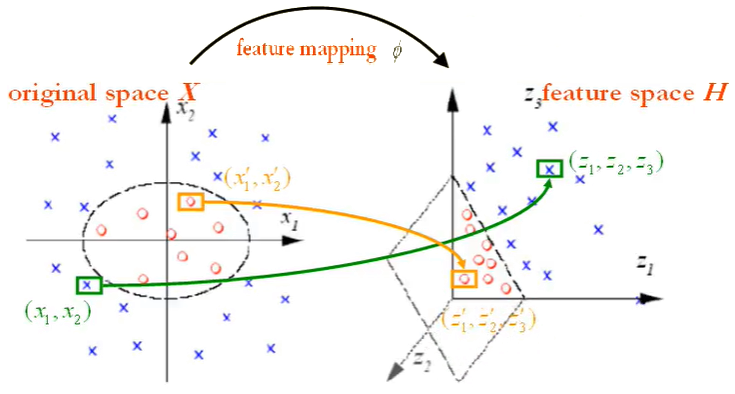
如上图所示，原$R^2$空间$X$中的红蓝两类样本点$\mathbf{x}$（由两个分量构成$\mathbf{x}=[x_1,x_2{]}^T$）可以由一个椭圆曲线$\frac{x_1^2}{a^2}+\frac{x_2^2}{b^2}=1$非线性地分开，我们可以找到一个非线性映射$\varphi :{R^2}_{(x_1,x_2)}\to {R^3}_{(z_1,z_2,z_3)=(x_1^2,\sqrt{2}{x}_1{x}_2,x_2^2)}$，使得红蓝样本点在$R^3$目标空间$H$中可以由一个超平面线性分开，这时，显然空间$X$中的椭圆曲线转变为了$H$中的一条直线$\frac{1}{a^2}\cdot z_1+0\cdot z_2+\frac{1}{b^2}\cdot z_3=1$，经过它的一个线性超平面可以正确划分两类数据点，到此，你可能会产生一个问题，即这个映射是怎么找到的？

事实上，该问题基本是无解的，我们很难找出确切的映射函数，但是可以将问题进行转化，根据核相关理论，任意非线性映射$\varphi$必然对应有一个核函数$k$，同时给定一个核函数$k$（对应核矩阵需满足有限半正定的条件）就能构建出一个映射空间$H$（指高维希尔伯特空间Hilbert Space），且$H$中的两个样本点内积可以由其在原始空间中的向量表示通过核函数计算得出，即$<\varphi ({\mathbf{x}}_1),\varphi ({\mathbf{x}}_2)>=k({\mathbf{x}}_1,{\mathbf{x}}_2)$，$<\varphi ({\mathbf{x}}_1),\varphi ({\mathbf{x}}_2)>=\varphi ({\mathbf{x}}_1{)}^T\varphi ({\mathbf{x}}_2)=\varphi ({\mathbf{x}}_2{)}^T\varphi ({\mathbf{x}}_1)$为向量内积，因此我们要做的是将进行了核扩展的模型目标函数使用核函数$k$表示出来，以避免出现不可解的$\varphi$，那么这个核扩展目标函数该如何定义？以上述二分类为例，给定训练样本集$\{({\mathbf{x}}_{\mathbf{i}},y_i){\}}_{i=1,...,N}$，其中${\mathbf{x}}_{\mathbf{i}}\in R^n$，$y_i=\{+1,-1\}$为类别标签，其在非线性映射空间$H:R^m$中的表示为$\{(\varphi ({\mathbf{x}}_{\mathbf{i}}),y_i){\}}_{i=1,...,N}$，设在$H$中能够线性划分样本集的超平面为$l:{\mathbf{w}}^T\varphi (\mathbf{x})+b=0$，相应的二分类判别模型为$D(\mathbf{x})=\{\begin{array}{l}+1,{\mathbf{w}}^T\varphi (\mathbf{x})+b>0\\ -1,{\mathbf{w}}^T\varphi (\mathbf{x})+b<0\end{array}$，其中$\mathbf{w}\in R^m$，而根据表示理论，$\mathbf{w}$可以由$H$中训练样本的线性组合构成，设为$\mathbf{w}=\sum _{i=1}^N{a}_i\varphi ({\mathbf{x}}_{\mathbf{i}})=\varphi (\mathbf{X})\mathbf{a}$，其中$\varphi (\mathbf{X})=[\varphi ({\mathbf{x}}_1),...,\varphi ({\mathbf{x}}_{\mathbf{N}})]\in R^{m\times N}$，$\mathbf{a}=[a_1,...,a_N{]}^T\in R^N$，于是$l:{\mathbf{a}}^T[{\varphi }^T({\mathbf{x}}_1)\varphi (\mathbf{x}),...,{\varphi }^T({\mathbf{x}}_{\mathbf{N}})\varphi (\mathbf{x}){]}^T+b={\mathbf{a}}^T[k({\mathbf{x}}_1,\mathbf{x}),...,k({\mathbf{x}}_{\mathbf{N}},\mathbf{x}){]}^T+b=0$，由此，问题由求解未知量$\mathbf{w},b$变为求解未知量$\mathbf{a},b$，因为通常核函数所对应的高维映射空间维度$m$非常大（甚至是无穷维），远远大于训练样本数$N$，因此引入核函数极大减小了优化代价（未知参数量减少）。接下来的问题就简单了，我们采用Logistic回归构造二分类的目标函数（代价函数），得到$J=\frac{1}{N}\sum _{i=1}^N\ln (1+e^{-y_{i}f({\mathbf{x}}_{\mathbf{i}})})$，其中$f({\mathbf{x}}_{\mathbf{i}})={\mathbf{a}}^T[{\varphi }^T({\mathbf{x}}_1)\varphi ({\mathbf{x}}_{\mathbf{i}}),...,{\varphi }^T({\mathbf{x}}_{\mathbf{N}})\varphi ({\mathbf{x}}_{\mathbf{i}}){]}^T+b={\mathbf{a}}^T[k({\mathbf{x}}_1,{\mathbf{x}}_{\mathbf{i}}),...,k({\mathbf{x}}_{\mathbf{N}},{\mathbf{x}}_{\mathbf{i}}){]}^T+b={\mathbf{a}}^T{\mathbf{K}}_{:,i}+b$，其中$\mathbf{K}$为核矩阵，$\mathbf{K}={\varphi }^T(\mathbf{X})\varphi (\mathbf{X})=\left[\begin{array}{ccc}k({\mathbf{x}}_1,{\mathbf{x}}_1)& \cdots & k({\mathbf{x}}_1,{\mathbf{x}}_{\mathbf{N}})\\ ⋮& \ddots & ⋮\\ k({\mathbf{x}}_{\mathbf{N}},{\mathbf{x}}_1)& \cdots & k({\mathbf{x}}_{\mathbf{N}},{\mathbf{x}}_{\mathbf{N}})\end{array}\right]\in R^{N\times N}$，参数$\mathbf{a},b$的求解仍可借助感知器通过梯度下降优化算法得到，此时，感知器的输入变为$\{\mathbf{K}\}$，也就是原本的训练集$\{({\mathbf{x}}_{\mathbf{i}},y_i){\}}_{i=1,...,N}$转变为$\{({\mathbf{K}}_{:,i},y_i){\}}_{i=1,...,N}$，$\mathbf{a},b$变成感知器的权重以及偏置参数

测试阶段，给定测试样本点$\mathbf{x}\notin \{\mathbf{X}\}$，其所属类别将由判别模型$D(\mathbf{x})$，其中${\mathbf{w}}^T\varphi (\mathbf{x})+b={\mathbf{a}}^T[k({\mathbf{x}}_1,\mathbf{x}),...,k({\mathbf{x}}_{\mathbf{N}},\mathbf{x}){]}^T+b$计算得出

案例2：核PCA

案例3：核SVM（笔记）